
Trong đề toán, có bài tập như sau: “Hãy cho biết có tất cả bao nhiêu số có 3 chữ số mà các chữ số của những số đó đều lớn hơn 4”, bạn đã biết cách giải chưa? Bạn sẽ giải chúng như thế nào? Đừng lo lắng vì trong bài viết dưới đây chúng tôi sẽ cung cấp lời giải, dạng đề cũng như các cách giải dạng toán này một cách chi tiết.
Lời giải cho bài toán: “hãy cho biết có tất cả bao nhiêu số có 3 chữ số mà các chữ số của những số đó đều lớn hơn 4”
Đây là dạng toán tạo lập số tự nhiên, để giải được các dạng toán này chúng ta cần phải hiểu được yêu cầu của đề bài, dựa trên về cấu tạo số tự nhiên để có thể lập được kết quả đúng. Lưu ý nhỏ là khi lập số, chúng ta nên lập theo thứ tự từ nhỏ đến lớn hoặc ngược lại để tránh sai sót.
Lời giải cho bài toán trên như sau:
Bước 1: Liệt kê các số lớn hơn 4 lần lượt là: 5,6,7,8,9.
Bước 2: Tạo lập số như sau:
- có 5 cách chọn hàng trăm.
- có 5 cách chọn hàng chục.
- có 5 cách chọn hàng đơn vị.
Có 5 cách chọn hàng trăm, hàng chục và hàng đơn vị vì 5 số trên đều lớn hơn 4 nên khi tạo ra bất kỳ số nào thì cũng đều thỏa mãn được yêu cầu của bài toán.
Bước 3: Vậy số lượng số hạng có 3 chữ số mà các chữ số của những số đó đều lớn hơn 4 là:
5 x 5 x 5 = 125 (số)
Đáp án: 125 số.
Mục Lục
Các phương pháp giải dạng toán “Tạo lập các số tự nhiên”
Phương pháp Liệt kê
Đây là cách giải đơn giản nhất nhưng mất khá nhiều thời gian và dễ bị sai sót trong quá trình sai sót, đòi hỏi phải cẩn thận, tỉ mỉ. Phương pháp này nên áp dụng đối với các bài toán có yêu cầu không cầu kì.
Ví dụ:
Cho 3 chữ số 3; 4; 5. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?
Lời giải:
345, 354, 543, 534, 435, 453.
Vậy có 6 số tự nhiên có 3 chữ số khác nhau được lập từ 3 chữ số 3; 4; 5.
Đáp số: 6 số
Phương pháp tính cách chọn
Cách này dựa trên các dữ liệu được phân tích trên đề bài, từ đó tính ra các cách chọn đối với các hàng trăm, chục, đơn vị. Phương pháp này giúp giải toán nhanh chóng và ít sai sót hơn liệt kê.
Ví dụ:
Cho 4 chữ số 0; 1; 7; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?
Ở các bài cho thêm số 0 thì ta cần phải lưu ý vì số 0 không thể đặt ở hàng cao nhất đối với số tự nhiên. Vì ví dụ như số có 3 chữ số không thể là 045.
Lời giải:
Với 4 chữ số 0, 1, 7, 3 ta có:
- Có 3 cách chọn số cho hàng trăm ( vì không tính số 0).
- Có 3 cách chọn số cho hàng chục.
- Có 2 cách chọn số cho hàng đơn vị.
Vậy số lượng số tự nhiên có 3 chữ số khác nhau là:
3 x 3 x 2 = 18 (số)
Đáp số: 18 số
Phương pháp lập sơ đồ hình cây
Mục đích lập sơ đồ hình cây ở đây để giúp chúng ta có thể liệt kê các số theo hàng trăm, hàng chục, hàng đơn vị chính xác hơn và dễ dàng hơn trong việc kiểm tra, phát hiện ra những sai sót trong việc lập số.
Ví dụ:
Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số?
Chúng ta lập sơ đồ cây như hình sau:
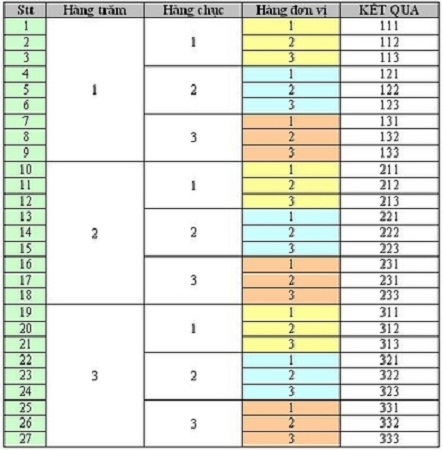
Theo dõi sơ đồ, ta có thể thấy được có 3 cách chọn số ở hàng trăm, 3 cách chọn số ở hàng chục và 3 cách chọn ở hàng đơn vị:
Do đó, số lượng số tự nhiên có 3 chữ số khác nhau sẽ là:
3 x 3 x 3 = 27 (số)
Đáp án: 27 số
Một số bài toán dạng tạo lập số
Bài 1
Cho 5 chữ số sau 7, 8, 3, 6, 2 bạn có thể viết được bao nhiêu chữ số thỏa mãn các yêu cầu sau:
- Có 3 chữ số
- Có 3 chữ số khác nhau.
Lời giải
- Với 5 chữ số trên, ta có:
- Có 5 cách chọn cho chữ số hàng trăm.
- Có 5 cách chọn cho chữ số hàng chục.
- Có 5 cách chọn cho chữ số hàng đơn vị.
Vậy số lượng số tự nhiên có 3 chữ số được tạo từ 5 số trên là:
5 x 5 x 5= 125 (số)
- Với 5 chữ số trên, ta có:
- Có 5 cách chọn cho chữ số hàng trăm.
- Có 4 cách chọn cho chữ số hàng chục.
- Có 3 cách chọn cho chữ số hàng đơn vị.
Vậy số lượng số tự nhiên có 3 chữ số khác nhau được tạo từ 5 số trên là:
5 x 4 x 3 = 60 (số)
Đáp án: a. 125 số b. 60 số
Bài 2
Cho 5 chữ số 0, 1, 8, 3, 5 em viết được bao nhiêu số có 3 chữ số khác nhau?
Lời giải:
Với 5 chữ số trên, ta có:
- Có 4 cách chọn cho chữ số hàng trăm.
- Có 4 cách chọn cho chữ số hàng chục.
- Có 3 cách chọn cho chữ số hàng đơn vị.
Vậy số lượng số có 3 chữ số thỏa mãn đề bài là:
4 x 4 x 3 = 48 (số)
Đáp số: 48 số
Bài 3
Trên kệ sách gồm 6 quyển sách tiếng Trung, 6 quyển sách Lý và 10 quyển sách Ngữ Văn. Lưu ý, các quyển sách này là hoàn toàn khác nhau. Hỏi:
- Có bao nhiêu cách chọn 1 quyển sách.
- Có bao nhiêu cách chọn 3 quyển sách khác môn học.
- Có bao nhiêu cách chọn 2 quyển sách khác môn học.

Lời giải:
- Số cách chọn 1 quyển sách là:
6 + 6 + 10 = 22 (cách)
- Số cách chọn 3 quyển sách khác môn học là:
6 x 6 x 10 = 360 (cách)
- Số cách chọn 2 quyển sách khác môn học là:
(6 x 6) + (6 x 10) + (6 x 6) = 132 (cách)
Đáp số: lần lượt là 22, 360, 132 cách.
Bài viết trên đã cung cấp lời giải cho đề bài: “Hãy cho biết có tất cả bao nhiêu số có 3 chữ số mà các chữ số của những số đó đều lớn hơn 4” và chi tiết cách giải dạng toán tạo lập số. Hy vọng đó sẽ là những kiến thức bổ ích đến bạn!







